CodeIQ 挑戦の記録 : 今週のアルゴリズム : 第88回「永遠に続くビリヤード」
CodeIQというサイトで問題に挑戦した記録です。
問題文を要約すると下記の通り、
- ビリヤードについて考える。クッションに対して45度の角度にボールを打つとする。
ボールの勢いが十分強くクッションに反射して同じ場所を繰り返して動くものとする。 - 横にm個、縦にn個のマス目で任意の格子点から始め、通過したマス目の数をカウントする。
- 標準入力からm,nが与えられた時、通過するマス目の数の最小と最大を解答する。
- m,nはいずれも60以下の整数
方針
通過するマス目の数は下記の通り計算できる。
のとき
最小、最大ともの最大公約数が
以外のとき
最小は
最大はの最大公約数が
が互いに素のとき
最小、最大とも
上記の説明
 のときは最小、最大ともに
のときは最小、最大ともに である。
である。
次に、 のとき、
のとき、
最小は

最大はである。

 のいずれかがもう片方の倍数になっている場合、
のいずれかがもう片方の倍数になっている場合、
仮にとすると、
最小は
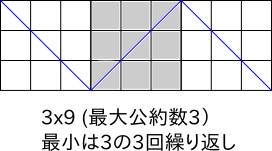
最大は
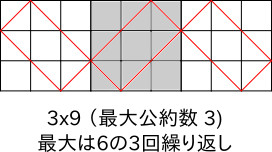
上記の他で最大公約数が1でない場合、
最小は

最大は
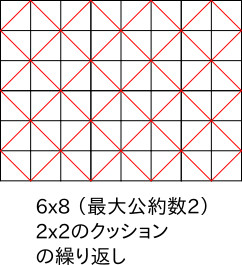
互いに素のとき、
最小、最大とも
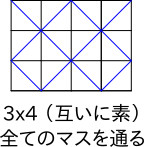
実装
上記を利用して提出したコード (Ruby)
では、
Sponsored Link
