CodeIQ 挑戦の記録 : 第75回「今週のアルゴリズム:たくさん配るサンタクロース」
CodeIQというサイトで問題に挑戦した記録です。
第75回「今週のアルゴリズム:たくさん配るサンタクロース」
問題文は正解者発表ページを参照下さい。
格子状のルートを同じ辺を通らずスタート地点に戻る通り方の内、最も長い通り方を求める問題。
今回は一筆書きの問題として考える。
連結グラフにおいて、一筆書きが可能かどうかの条件をWikipediaから引用。
ある連結グラフが一筆書き可能な場合の必要十分条件は、以下の条件のいずれか一方が成り立つことである(オイラー路参照)。
- すべての頂点の次数(頂点につながっている辺の数)が偶数 →運筆が起点に戻る場合(閉路)
- 次数が奇数である頂点の数が2で、残りの頂点の次数は全て偶数 →運筆が起点に戻らない場合(閉路でない路)
ある点からスタートし、一筆書きをしてスタート地点に戻ってきて終わる事ができる必要十分条件は全ての頂点につながっている辺の数が偶数である事である。
頂点につながっている辺の数が奇数のものを「奇点」と呼ぶ事にする。
今回の問題は最大の経路を求めるものであるが、最も効率良く奇点を取り除き、一筆書きができる中で、通らない辺の数が最も少なくなるものを数えてその数を解答とする。
アルゴリズム
奇点について
格子状のグラフの場合、奇点は外周部にしかなく、四隅を除く外周部の頂点は全て奇点になっている。
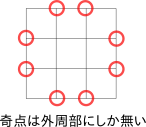
奇点と奇点の間の辺を取り除くと両端の頂点は奇点ではなくなるので、外周部に沿って、奇点と奇点の間の辺を 一つおきに取り除いていく事にする。

但し、取り除く辺が四隅の辺の内の一辺であった場合、もう片方の辺は通れなくなる為四隅の辺の場合はその両方を取り除く。
縦・横の辺の数によって場合分けをする。
- 縦・横のいずれかの辺の数が0の場合 一筆書きで戻る事はできないので、0を解答とする

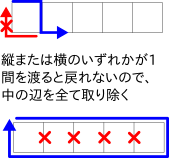
- 縦・横のいずれかの辺の数が1の場合
内部にある辺を1回でも渡るとスタート地点に戻れないので、全ての辺の数から内部の辺の数を引いた数を解答とする。
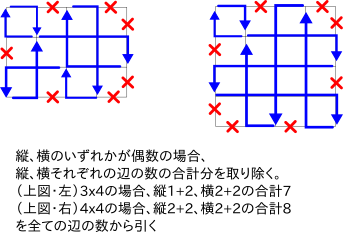
- 縦・横のいずれかが偶数の場合
縦・横の辺の数の合計を全ての辺の数から引いた数を解答とする。
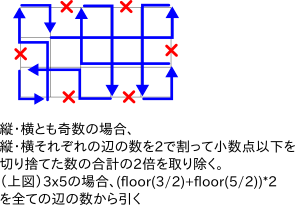
- 縦・横のいずれもが奇数の場合
縦・横それぞれの辺の数を2で割り、小数点以下を切り捨てた数の合計の2倍を全ての辺の数から引いた数を解答とする。
コード
提出したコードは下記の通り(Ruby)