CodeIQ 挑戦の記録 : 今週のアルゴリズム : 第93回「ナルシストなナルシシスト数」
CodeIQというサイトで問題に挑戦した記録です。

問題文を要約すると下記の通り
- ナルシシスト数に関する問題。
(ウイキペディアより引用)
n桁の自然数であって、その各桁の数のn乗の和が、元の自然数に等しくなるような数をいう。例えば、
であるから、153 はナルシシスト数である。
十進法に限らず、他の基数においても同様にナルシシスト数を定義できる。
- 標準入力から nが与えられる。n進数で2桁以上のナルシシスト数を小さい方からn個求め、標準出力にn進数で順に出力する。
- nは10以下の整数。
方針
全探索()するより他に良い方法を思いつかなかった。
しかしながら、問題文より、答えを10個出力すれば打ち切れるので全探索をする事にした。
サンプルとして10進法の例が書かれてあり、10進法での10個目の答えは「93084」となっているので、(組み込み関数の内部処理を無視すれば)nの最大で約93,000回ほどのループ(x定数倍)で答えがでる。
その他の基数でのナルシシスト数の個数は不明で、10個に満たない場合、最悪のケースで=約3億8千万回ループする可能性があるが、それで時間制限に間に合わなかった場合は、改めて考え直す事にした。
実装してからローカルでテストすると、十分間に合ったのでそのまま提出した。
(提出結果はのケースで約0.3秒で正解)
なお、rubyでは
- 10進法の数値を任意のn進法の文字列に変換して表示するメソッド
- n進法の文字列を10進法の数値に変換するメソッド
をともに備えているので、これを利用し、n進法で2桁の最小値()からn桁の最大値(
)までの整数を都度n進法に変換し比較、ナルシシスト数と一致したものを出力した。
組み込み関数を用いればRubyでの実装は簡単であった。
実装(Ruby)
では、
Sponsored Link
CodeIQ 挑戦の記録 :「レッド・アンド・ホワイト」問題
CodeIQというサイトで問題に挑戦した記録です。
問題文を要約すると下記の通り
- マス目が直線上に限りなく並んでいる(初期状態は全て白色)
- このうちの1つを赤色に塗る。
- 次のルールに従いマス目の色を塗り替える時、n秒後の赤色のマス目の個数を解答する。
- 1秒ごとに下記の通り変化する
左右のマス目が白赤または赤白のマス目->赤色に塗る。
左右のマス目が白白または赤赤のマス目->白色に塗る。
方針
題意に従い、二次元配列を使って状態の変化を表示してみる。
赤色のマス目を「1」で、白色のマス目を空白で表示すると、パスカルの三角形に似た図形が表示される。

この図形は、パスカルの三角形の奇数部分を塗りつぶしてできる「シェルピンスキーのギャスケット」と同様のものである。
パスカルの三角形には様々な規則性が隠れているが、n行目(最初を0行目とする)に含まれる奇数の個数はnを2進法で表記した時の1の個数をとすると
に等しい事が知られている。
[パスカルの三角形と2進法]
http://www7b.biglobe.ne.jp/~fukagawa/documents/mod2pascal.pdf
実装
上記の性質を用いて解答する。(Ruby・27文字)
なお、標準入力からの数値を2進法で文字列化する時に、Rubyではsprintfが使えるが、これの代わりに「%」で書式文字列が使えるのでこれを利用して2進法表記の文字列とし、その中の1を数えている。
p 2**(("%b"%gets).count'1')
おまけ
上記の規則性に気づく前に提出した1回目の解法
この三角形は0行目が1が1個、1行目が1が2個の2行でなる三角形が2行ごとに2倍ずつ繰り返し現れ、
2のべき乗行目に2に戻る事を繰り返している。
これより、与えられた数をその数より小さい最大の2のべき乗で引いていき、その回数の2倍を解答とする。
n=gets.to_i;a=1;while n>0;a*=2;n-=2**Math.log2(n).floor;end;p a
では、
Sponsored Link
CodeIQ 挑戦の記録 : 今週のアルゴリズム : 第92回「最短距離で往復できる形は?」
CodeIQというサイトで問題に挑戦した記録です。

問題文を要約すると下記の通り
- 格子状の道路があり、左下のA点から右上のB点まで最短距離で移動し、A-B点の移動を繰り返す。
- このとき、一度通ったルートは通らず全てのパターンを通ったとき、最終的にA点で終わる場合を考える。
- A-B間の移動距離nが標準入力から与えられたとき、最終的にA点で終わる形のうち、横幅が最小になるものを解答する。
- A点で終わるものがない場合は0を出力する。

方針
幅、高さ
の格子状の対角線上の位置
を最短距離で移動する時の場合の数は
組み合わせ ( =
) 通りである。
を往復し全てのルートを通って出発地点に戻るためにはこの組み合わせが偶数であれば良い。
これより、問題の距離を幅から始めて場合の数が最初に偶数になる幅を解答とする。
の値が最初に偶数になる
を探すが、普通に計算すると大きい入力で計算値が大きくなりすぎ、時間がかかるため、分母・分子をその都度最大公約数で割り(約分)、分子が最初に偶数になった時の回数を解答とする。
実装(Ruby)
では、
Sponsored Link
(JavaScript) アスタリスクで菱形を書いてみた
こんなブログを見かけた。
未経験でWebエンジニアになって1ヶ月の人が、どういう訳か、JavaScirpt、アスタリスクで菱形を表示する事になったらしい。
表示するのはこんなの、

面白そうなのでやってみた。
問題の仕様
- JavaScript
- for文を使う
- console.logでアスタリスクを使って表示する
方針
5行9列の場合でアスタリスクを表示する位置は
(0,4)
(1,2),(1,3),(1,4),(1,5),(1,6)
(2,0), .. ,(2,8) (2行全て)
(3,2),(3,3),(3,4),(3,5),(3,6)
(4,4)
この場合のアスタリスクを表示する位置を数式で表すと、
行(i)が0から4、列(j)が0から8の範囲で(i,j)について、
<
( | | は絶対値)
が成立する時である。
実装 JavaScript (Node.js)
上記の数式を用いて実装する。
- 上記の例では5行のみだが、定数を変更する事により任意の奇数行で表示できる様にしてある。
- 実行環境はideone.com上でNode.jsとして可能(console.logを使用するので)のほか、htmlに埋め込んでFirefoxのFirebugでも動作確認済み。
- コードはGistに埋め込み
では、
Sponsored Link
CodeIQ 挑戦の記録 : 今週のアルゴリズム : 第91回「最短で当たるビンゴゲーム」
CodeIQというサイトで問題に挑戦した記録です。

問題文を要約すると以下の通り、
- ビンゴカードの数字が4枚分標準入力より与えられる。
- この数字は1から75までの整数で、1枚の中では同じ数字が2回現れる事はない。
- 一般的なビンゴカードと違い真ん中のマスも「FREE」ではなく数字が書かれている。
- 4枚全てがビンゴになる時、出る数字の種類が最も少ない場合の数字の個数を解答する。
方針
マスのカードのビンゴになる並びは縦・横・斜めの
通りである。
全てのカードについて全ての並びの組み合わせを試しても通りなので1秒の時間制限にも十分間に合う。
なので、全ての組み合わせを試し、その中で最も数字の種類の少ないものを選んで解答する事とする。
なお、数字の種類を数える方法は、組み合わせの数字全てをハッシュに代入し、ハッシュのサイズで比較する事にする。
全ての組み合わせを試す方法としては、4重ループにせず、再帰を用いた。
再帰を用いた方法であれば、時間はかかるが、カードが何枚でもコードを修正せずに答えを出せる。
実装 (Ruby)
Sponsored Link
CodeIQ 挑戦の記録 : 今週のアルゴリズム : 第89回「一筆書きの交点」
CodeIQというサイトで問題に挑戦した記録です。

問題を要約すると以下の通り、
- 円周上に等間隔にn個の点がある。
- 任意の点から一筆書きで最初の点へ戻るルートを考えた時、交差する回数の総計を解答する。
- nの最大値は9
方針
今回は規則性を見つける事ができず、全探索を行うしかなかった。
当初、時間制限に間に合わないのを確認しながらRubyで提出、TLEだったので、
C++でほぼ同じコードを書き直し再提出。正解した。
(順列の生成に、Rubyでは Array#permutation を使用。C++では自前で実装。
ちなみにn=9の場合で、RubyではTLE、C++では表示0.0秒。事前の「実行くん」では0.02秒)
なお、組み合わせにより式を導いた@angel_p_57さんの解説はこちら、
素晴らしい。
実装
C++ (gcc 4.9.3)
では、
Sponsored Link
CodeIQ 挑戦の記録 : 今週のアルゴリズム : 第88回「永遠に続くビリヤード」
CodeIQというサイトで問題に挑戦した記録です。
問題文を要約すると下記の通り、
- ビリヤードについて考える。クッションに対して45度の角度にボールを打つとする。
ボールの勢いが十分強くクッションに反射して同じ場所を繰り返して動くものとする。 - 横にm個、縦にn個のマス目で任意の格子点から始め、通過したマス目の数をカウントする。
- 標準入力からm,nが与えられた時、通過するマス目の数の最小と最大を解答する。
- m,nはいずれも60以下の整数
方針
通過するマス目の数は下記の通り計算できる。
のとき
最小、最大ともの最大公約数が
以外のとき
最小は
最大はの最大公約数が
が互いに素のとき
最小、最大とも
上記の説明
 のときは最小、最大ともに
のときは最小、最大ともに である。
である。
次に、 のとき、
のとき、
最小は

最大はである。

 のいずれかがもう片方の倍数になっている場合、
のいずれかがもう片方の倍数になっている場合、
仮にとすると、
最小は
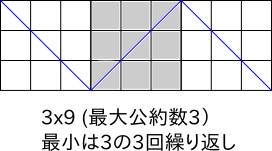
最大は
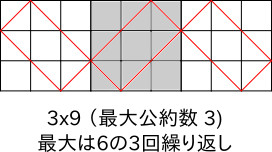
上記の他で最大公約数が1でない場合、
最小は

最大は
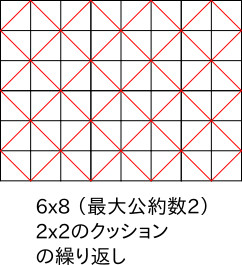
互いに素のとき、
最小、最大とも
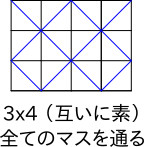
実装
上記を利用して提出したコード (Ruby)
では、
Sponsored Link
